Als er een kortsluiting is in het elektriciteitsnet gaat er een grote stroom lopen, de kortsluitstroom. Deze stroom gaat dan ook door de transformator en die dient daar tegen te kunnen. Deze grote stroom resulteert namelijk in grote Lorentz krachten in de wikkelingen.
- De HS ( hoogspannings) wikkeling ondervindt een radiale kracht naar buiten toe en wil dus een grotere diameter krijgen. Die drukkracht is goed te beheersen, denk maar aan een plastic fles waarin je lucht blaast. Blijft mooi heel en rond.
- De LS ( laagspannings) wikkeling ondervindt een radiale kracht naar binnen toe en wil dus een kleinere diameter krijgen. Die vacuümkracht is moeilijk te beheersen, denk maar als je de lucht uit een plastic flesje zuigt. De fles gaat plotseling ergens veel vervormen en dat noemt men knikken ( zie fig 2 maar kijk ook eens op youtube – buckling of plastic bottle ). Het vereist uitvoerige proeven ( zie fig 1 ) om ontwerp criteria te bepalen voor de radiale kortsluitvastheid van LS-wikkelingen.
 |
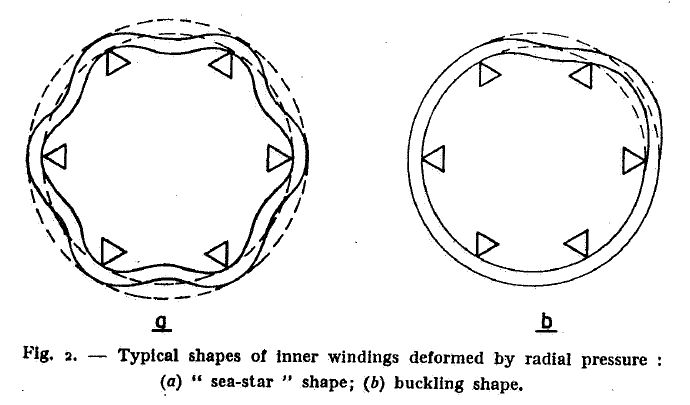 |
| Fig 1 De kop van het artikel. Gepubliceerd in 1962 op een internationaal congres van Cigre | Fig 2 Knikvormen van de LS wikkeling. Het zeesterren tussen alle spiëen en de willekeurige knikvorm met een spie als “draaipunt”. |

Fig. 3 Zo ziet knikken er ook uit als de rails te heet wordt en dan uitzet. Als de rails niet kan uitzetten dan ontstaat in het staal een grote drukspanning. Als de druk te hoog wordt, knikt de rails.
( zoek voor “leuke” foto’s op internet naar : knikken van spoorrails) --->
Het kortsluitapparaat – een revolutionair idee van R. Boersma en J. Wildeboer
 Boersma en J. Wildeboer (zie foto) bedachten een apparaat dat hetzelfde magnetische veld maakt in de wikkelingen als bij de kortsluitstroom. Je krijgt dan dezelfde kortsluitkrachten, maar in dit apparaat hebt je maar een klein stukje hoogte van de wikkelingen nodig.
Boersma en J. Wildeboer (zie foto) bedachten een apparaat dat hetzelfde magnetische veld maakt in de wikkelingen als bij de kortsluitstroom. Je krijgt dan dezelfde kortsluitkrachten, maar in dit apparaat hebt je maar een klein stukje hoogte van de wikkelingen nodig.
Het werkt als volgt : Je wikkelt twee dubbelspoelen met een totale hoogte van 90 mm en een gemiddelde diameter van 770 mm. Dat vormt de LS-wikkeling. De HS-wikkeling maak je ook zo maar dan met iets sterkere geleider en met een gemiddelde diameter van 890 mm. Je hebt zo een “schijfje” uit de wikkelingen, maar veel goedkoper en ook veel gemakkelijker te beproeven. Deze wikkelingen zitten opgesloten in een “kern” waarbij hetzelfde magnetische veld ontstaat als in de transformator. ( zie fig 4 en fig 9 ).
Deze “kern” bestaat uit een onder- en bovenjuk ( zie fig 5 ). De LS wikkeling is gepositioneerd op het onderjuk. Het zit om een kern van kernblik met een houten opvulring. ( zie fig 6 ) Zo simuleer je de kern van de transformator en de afsteuning van de LS wikkeling op de kern via kernspieën. De HS wikkeling zit gemonteerd tegen het bovenjuk en aan de buitenzijde van de HS wikkeling zit een cilinder van kernblik. Zo kan het magnetische veld zich goed sluiten ( zie fig 9 ).
Opm : De spoelhoogte is normaal in de ordegrootte van 1000 mm tot 2000 mm.
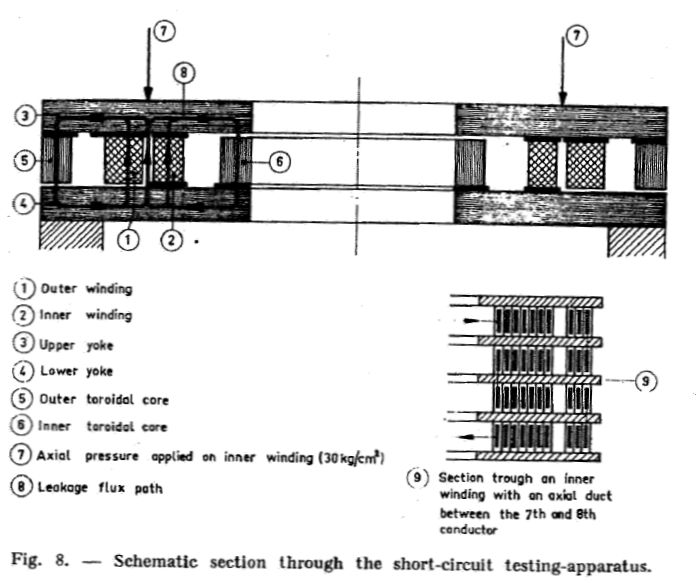
Fig 4 Doorsnede van kortsluitapparaat
Fig 5 Radiaal gestapeld juk. Onder en bovenjuk zijn hetzelfde. De monteur is (zeer waarschijnlijk) Jan Huijding.

Fig 6 Een LS wikkeling gemonteerd op het onderjuk. Van binnen naar buiten :
- De kern in de vorm van gewikkeld kernblik. ( Nr 6 op fig 4 )
- Houten opvulring met steunblokken om de ondersteuning via kernspieën te simuleren
- De LS wikkeling ( Nr 2 op fig 4 )

Fig 7 Het kortsluitapparaat in geopende toestand. Op de voorgrond het onderjuk gemonteerd op een aandrukconstructie om het bovenjuk tegen het onderjuk te drukken. Op de achtergrond ligt het bovenjuk
Het bekijken van de LS wikkelingen na een “schot” ( dat betekend dat er een kortsluitstroom door de wikkelingen heeft gelopen en dat geeft een aardige knal ) is eenvoudig uit te voeren. Je maakt de trekstangen los en tilt vervolgens het bovenjuk op via het hijsoog.
Testresultaten.
De LS wikkelingen zijn gemaakt van koperdraad ( 1,4 mm x 15 mm ) dat geïsoleerd is met lak. De 0,2% permanente rekgrens ( sigma0,2 ) is 90 N/mm2 en dus zacht koper. Latere proeven met het kortsluitapparaat, die uitgevoerd zijn door A. Bose in 1970, was heel zacht koper gebruikt met een sigma0,2 grens van 70 N/mm2.

Fig 10 Het zeesterren van de wikkeling. Wikkeling is gedemonteerd uit kortsluitapparaat.

Fig 11 Zeesterren van de wikkeling – detail. Wikkeling zit nog op onderjuk gemonteerd.
 |
 |
||
|
|
 |
 |
||
|
|
Hoe ziet dat eruit in een transformator.
In die tijd zijn er ook kortsluitproeven gedaan aan een aantal kleine transformatoren. ( fig 13 en fig 14 ) . Je wilt toch ook zien of de resultaten uit het onderzoek ook zonder meer toepasbaar zijn in transformatoren. Ter illustratie wat foto’s van LS wikkelingen die beproefd zijn tot ze bezweken bij de kortsluitproef.
 |
 |
| Fig 16 Geknikte LS wikkelingen die nog om de kernpoot zitten. | Fig 17 Zeesterren van een LS wikkeling. |
Maar een transformator kan er na een kortsluiting ook uit zien zoals in fig 18. Een foto van een transformator die gefaald heeft na een kortsluiting. Het vereist detectivewerk om in deze berg “spaghetti” te achterhalen waar de fout is begonnen. Je kunt het vergelijken met het vinden van de plaats waar een brand is begonnen is, nadat het hele gebouw is afgebrand.
Het zoeken van een speld in een hooiberg lijkt er ook veel op en soms vindt je die ook niet.
Het meest vervelende is als je de bron van dit falen niet kunt vinden. Je hebt dan niets geleerd en je weet dan niet hoe je de transformator moet verbeteren.

In de periode 1998 tot 2000 is het onderzoek naar de kortsluitvastheid van LS wikkelingen weer opgestart en dat werd geleid door Rob Verhoeven. Het kortsluitapparaat ( fig 20 ) was anders van ontwerp en zonder magnetisch sluitjuk, maar de ideeën van Boersma en Wildeboer lagen hieraan echter ten grondslag. Deze proeven waren met name bedoeld om ontwerpcriteria te bepalen van LS wikkelingen met baklakkabel. Tevens was de hardheid van het koper, gegeven via de sigma0,2 grens, een parameter.
 |
 |
|
| Fig 19 Geknikte LS wikkeling na kortsluitproef bij de Kema in Arnhem. De spieën, die zorgen voor de afsteuning van LS wikkeling op de kern, hadden het begeven. Het gevolg : Knikken van de LS wikkeling. |
|
Voor leuke en spectaculaire filmpjes van transformatoren die falen na kortsluiting, wat ook kan door een interne fout in de transformator zelf. Dan zie je ook de spectaculaire kanten van ons vak.
Type zelf eens in bij Google : YouTube transformer on fire of Electrical Transformer Exploding
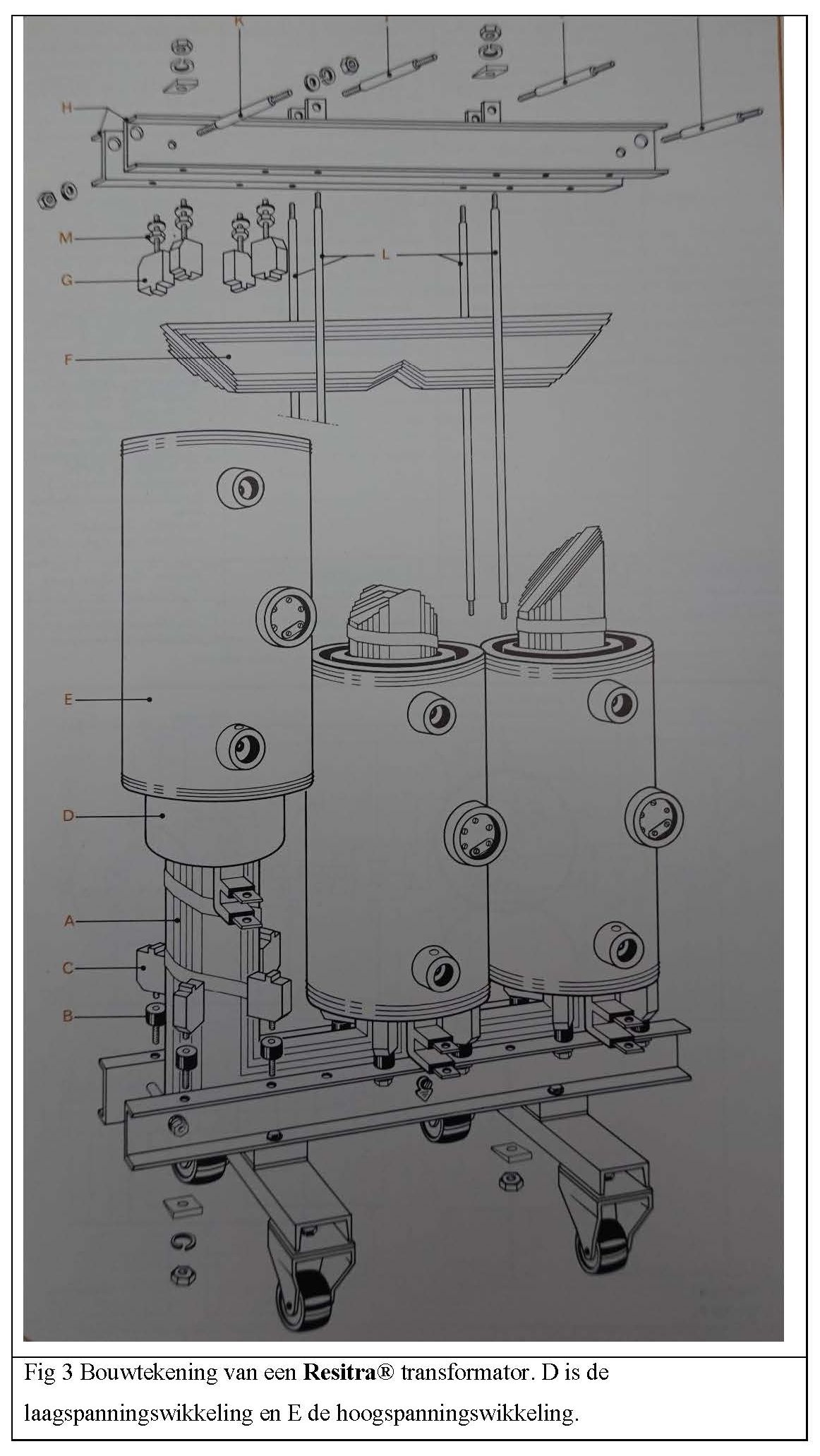
Bron: Archief Smit Transformatoren, Stichting Willem Smit Historie Nijmegen.




















Reacties mogelijk gemaakt door CComment